VAEからCVAE with keras

はじめに

出てきた当初は画像分類タスクで猛威を振るった深層学習ですが, 最近はいろんな機械学習と組み合わせで応用されています. 強化学習を応用したAlphaGoでイ・セドルを打ち負かしたり, 画像認識と自然言語処理の組み合わせで画像のキャプションを生成したり, 生成モデルに応用して自然に近い画像を作るなど賑わいを見せています.

今回は画像生成手法のうちのDeepLearningを自然に生成モデルに拡張したと考えられるVAE(Variational Auto Encoder)から, その発展系であるCVAE(Conditional VAE)までを以下２つの論文をもとに自分の書いたkerasのコードとともに紹介したいと思います.

Auto-Encoding Variational Bayes
Semi-Supervised Learning with Deep Generative Models

VAE系手法の良い所

確率分布をニューラルネットワークを用いて表現できると次の２つの良い点があります.

サンプリングによって新たな画像(学習画像の生成分布に沿った)を生成することができる
潜在空間の変数をいじることによって狙った画像を生成したり画像どうしのアナロジーをみることができる

この２つの点はそのまま生成モデルの良い点だということができます. そこでまずは生成モデルとはなんなのか自分なりにまとめてみます.

生成モデル

抽象的な話をすると生成モデルでは観測されたデータ ${x}$ に対して, 非観測な潜在変数 ${z}$ を仮定し, ${z}$ が確率分布 ${p(z)}$ からサンプリングされ, 生成された ${z}$ を用いて ${p(x|z)}$ から ${x}$ が生成されたとして数理モデルに落とし込みます.
つまりそこにあるデータの背後にはなにか見えない変数が存在しそれをもとにデータが生成されたとする一種の考え方とも言えます.

具体的な例として高３男子の身長の分布を考えてみます. その分布の形状は正規分布に近い形になっていることが知られているので今回は正規分布を仮定して考えます. 確率分布は形状とパラメータで定まります. 形状は正規分布を仮定しているのでパラメータ ${\mu}$ と ${\sigma}$ を使って ${p(x|\mu, \sigma)=N(\mu, \sigma)}$ となります.
この ${\mu}$ と ${\sigma}$ をただのパラメータではなく確率変数(何かの分布に従っている)として ${\mu}$ と ${\sigma}$ を潜在変数とした生成モデルを考えることができます. ${\mu}$ と ${\sigma}$ には上の ${p(z)}$ にあたる事前分布が存在します.
図で書くと下のようになります.

f:id:ralo23:20160825203909p:plain

生成モデルではサンプリングを行えるので高３男子の身長のサンプルがほしい!となったら ${\mu}$ と ${\sigma}$ の事前分布から ${\mu}$ と ${\sigma}$ を生成し ${p(x|\mu, \sigma)}$ からサンプリングすればよいわけです. (このようなシチュエーションがあるかはしらない)
さらには確率を計算できるので適当な身長を ${p(x|\mu, \sigma)}$ の ${x}$ に代入してその身長が高３男子としてどれだけ確からしいかを数値として割り出すこともできます.

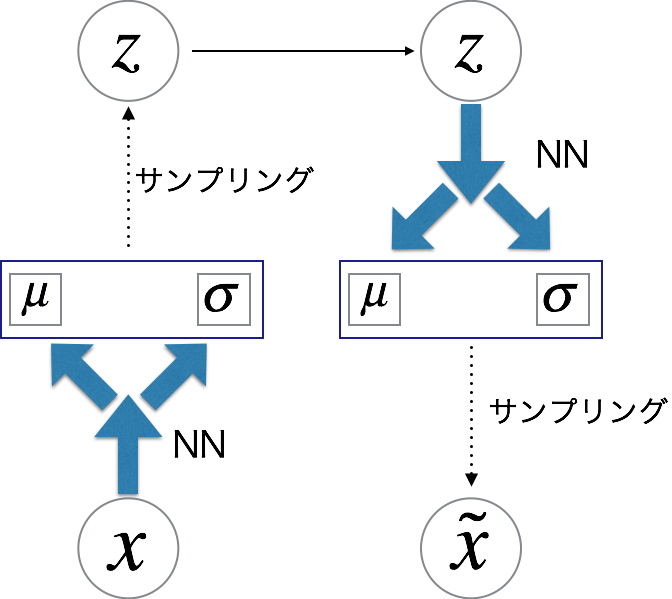
VAEとは

VAEでは生成モデルの枠組みをそのまま利用します. 学習するデータ(画像など)に対して潜在変数 ${z}$ を仮定し ${p(z)}$ から ${z}$ を生成し, ${p(x|z)}$ で ${x}$ が生成されたとします.
この ${p(x|z)}$ をNeuralNetworkで表現します.

確率分布をNNで表す

VAEでは確率分布のgivenな変数( ${p(x|z)}$ でいうところの ${z}$ )を引数に取り, 確率分布のパラメータを出力にするNeuralNetworkで確率分布を表現します. 形状はprioriで実験ではガウス分布やベルヌーイ分布を使用しています.

具体的にガウス分布でmnist(784次元)を考えてみると ${z}$ を入力にとって784次元の ${\mu}$ ベクトルと ${\sigma}$ ベクトルを出力します. 各次元に対して一次元ガウス分布のサンプリングを行うことで ${x}$ を生成できます.

確率分布の実装

確率分布のNNによる表現方法はきまったのでそれをどのように実装するかという話になります.
今回の実装ではkerasを使用したのでkerasのfunctionalAPIの機能をふんだんに使用しました.
functionalAPIについて詳しくはkeras tutorialを見てください.
Sequentialを使うことで入力, 出力をtensorに持つNeuralNetworkを１つの関数のように構築できます.

NeuralNetworkで表される条件付き確率分布の主要な機能としては,

givens()が与えられた時
- サンプリング
- パラメタ計算
givens()と確率変数()が与えられた時
- 確率の計算
- 対数尤度の計算

ができればよいのでそれをみたすクラスを作りました. initの引数でkerasのSequentialオブジェクトを与えます.

class GaussianDistribution(ProbabilityDistribution):
    def __init__(self, variable, givens=None, mean=0, var=1, mean_model=None, var_model=None):
        self.variable = variable
        self.variable_shape = K.int_shape(self.variable)
        def sample(args):
            mean, var = args
            epsilon = K.random_normal(K.shape(mean))
            return mean+var*epsilon
        self.draw = Lambda(sample)
        self.mean_model = mean_model
        self.var_model = var_model
        if givens is None:
            if isinstance(mean, float) or isinstance(mean, int):
                self.mean = K.ones_like(self.variable)*mean
            else:
                self.mean = mean
            if isinstance(var, float) or isinstance(var, int):
                self.var = K.ones_like(self.variable)*var
            else:
                self.var = var

    def get_params(self, givens=None):
        if givens is None:
            return self.mean, self.var
        mean = self.mean_model(givens)
        var = self.var_model(givens)
        return mean, var

    def sampling(self, givens=None):
        if givens is None:
            return self.draw([self.mean, self.var])
        mean = self.mean_model(givens)
        var = self.var_model(givens)
        return self.draw([mean, var])

    def prob(self, variable, givens=None):
        if givens is None:
            return 1/K.sqrt(2*np.pi*self.var)*K.exp(-1/2*(variable-self.mean)**2/self.var)
        mean = self.mean_model(givens)
        var = self.var_model(givens)
        return 1/K.sqrt(2*np.pi*var)*K.exp(-1/2*(variable-mean)**2/var)

    def _log_gausian(self, variable, mean, var):
        return -1/2*K.log(K.clip(2*np.pi*var, K._epsilon, 1/K._epsilon))-1/2*(variable-mean)**2/K.clip(var, K._epsilon, 1/K._epsilon)

    def logliklihood(self, variable, givens=None):
        """
        a mean logliklihood of minibatch
        """
        if givens is None:
            return K.mean(K.sum(self._log_gausian(variable, self.mean, self.var), axis=1))
        mean = self.mean_model(givens)
        var = self.var_model(givens)
        return K.mean(K.sum(self._log_gausian(variable, mean, var), axis=1))

このクラスを使って実装していきます.

cost関数

実装を始める前にcost関数を定める必要があります.
生成モデルでのコスト関数が ${-log p(x)}$ であることは問題ないと思います. 作った確率分布に対して, 実際のトレーニングデータ ${x}$ の生成される確率を計算し, その値が大きいほどその生成分布は実際のデータに即していると考えられるからです. ここでは負の対数を取ってあります.
この ${log p(x)}$ を式変形していき, 計算できる値まで持って行きます.

${ \begin{align} log p(x) &= log \int p(x, z) \mathrm{d}z \tag{1} \\ &= log \int p(x|z)p(z) \mathrm{d}z \tag{2} \\ &= log \int q(z|x)\frac{p(x|z)p(z)}{q(z|x)}\mathrm{d}z \tag{3} \\ &\geq \int q(z|x)log \frac{p(x|z)p(z)}{q(z|x)}\mathrm{d}z \tag{4} \\ &= \int q(z|x)log p(x|z)\mathrm{d}z-\int q(z|x)log \frac{q(z|x)}{p(z)}\mathrm{d}z \tag{5} \\ &= E_{z\sim q(z|x)} \left[ log p(x|z) \right ] - D_{KL} \left(\frac{q(z|x)}{p(z)} \right) \tag{6} \\ \end{align} }$

(1)は周辺化の定義式で, (2)はベイズの定理, (3)は ${q(z|x)}$ の導入, (4)はイェンゼンの不等式, (6)は期待値とKLダイバージェンスの定義式を利用して式変形しています.
急に出てきた ${q(z|x)}$ は代理分布と呼ばれ, ${p(x|z)}$ の計算が困難な場合に用いられます.

第一項の期待値は ${q(z|x)}$ からサンプリングした ${L}$ 個の点を用いて $\frac{1}{L}\sum^l logp(x|z_l)$ で近似できます. 論文中では大きなミニバッチサイズで計算することで ${L=1}$ でも良い結果が得られることが書いてあります.

第二項のKLダイバージェンスは解析的に計算することができ, $-\frac{1}{2} \sum^d(1+log(\sigma_d^2)-\mu_d^2-\sigma_d)$ となります.

この辺の式変形はAuto-Encoding Variational BayesのAppendixに詳しく書いてあるのと, 日本語の記事ではVariational Dropout and the Local Reparameterization Trickや正規分布間のKLダイバージェンスの導出を参考にしました.

実装

先ほど作ったNNを持つ確率分布のclassを使ってVAEclassを実装します.
確率分布がもつNNの構造をkerasのSequentialで記述し確率分布を生成し, その確率分布をもとに ${z}$ のサンプリングと ${x}$ の復元を行いcostを計算します.

f:id:ralo23:20160826130649p:plain

class VAEM1(object):
    def __init__(self, in_dim=784, hid_dim=300, z_dim=50):
        self.in_dim = in_dim
        self.hid_dim = hid_dim
        self.z_dim = z_dim
        self.x = Input((self.in_dim, ))
        self.z = Input((self.z_dim, ))

        ############
        # q(z | x) #
        ############
        model = Sequential()
        model.add(Dense(self.hid_dim, input_dim=self.in_dim))
        model.add(CustomBatchNormalization())
        model.add(Activation('softplus'))
        model.add(Dense(self.hid_dim))
        model.add(CustomBatchNormalization())
        model.add(Activation('softplus'))
        mean = Sequential([model])
        mean.add(Dense(self.hid_dim))
        mean.add(CustomBatchNormalization())
        mean.add(Activation('softplus'))
        mean.add(Dense(self.z_dim))
        var = Sequential([model])
        var.add(Dense(self.hid_dim))
        var.add(CustomBatchNormalization())
        var.add(Activation('softplus'))
        var.add(Dense(self.z_dim, activation='softplus'))
        self.q_z_x = GaussianDistribution(self.z, givens=[self.x], mean_model=mean, var_model=var)

        ############
        # p(x | z) #
        ############
        model = Sequential()
        model.add(Dense(self.hid_dim, input_dim=self.z_dim))
        model.add(CustomBatchNormalization())
        model.add(Activation('softplus'))
        model.add(Dense(self.hid_dim))
        model.add(CustomBatchNormalization())
        model.add(Activation('softplus'))
        model.add(Dense(self.in_dim, activation='sigmoid'))
        self.p_x_z = BernoulliDistribution(self.x, givens=[self.z], model=model)

        ########################
        #sample and reconstruct#
        ########################
        self.sampling_z = self.q_z_x.sampling(givens=[self.x])
        self.reconstruct_x = self.p_x_z.sampling(givens=[self.sampling_z])

    def _KL(self, mean, var):
        return -1/2*K.mean(K.sum(1+K.log(K.clip(var, K._epsilon, 1/K._epsilon))-mean**2-var, axis=1))

    def cost(self, inputs, outputs):
        mean, var = self.q_z_x.get_params(givens=[self.x])
        KL = self._KL(mean, var)
        logliklihood = self.p_x_z.logliklihood(self.x, givens=[self.sampling_z])
        lower_bound = -KL+logliklihood
        lossfunc = -lower_bound
        return lossfunc

    def training_model(self):
        model = Model(input=self.x, output=self.reconstruct_x)
        return model

    def encoder(self):
        model = Model(input=self.x, output=self.sampling_z)
        return model

    def decoder(self):
        decode = self.p_x_z.sampling(givens=[self.z])
        model = Model(input=self.z, output=decode)
        return model

トレーニングコードは以下のようになります.

from __future__ import division
from keras.datasets import mnist
from vae_m1 import VAEM1

nb_epoch = 30


if __name__ == '__main__':
    (X_train, y_train), (X_test, y_test) = mnist.load_data()
    X_train = X_train.reshape(-1, 28*28)
    X_test = X_test.reshape(-1, 28*28)
    X_train = X_train/255.0
    X_test = X_test/255.0
    X_train[X_train > 0.5] = 1.0
    X_train[X_train <= 0.5] = 0.0
    X_test[X_test > 0.5] = 1.0
    X_test[X_test <= 0.5] = 0.0


    vaem1 = VAEM1()

    training = vaem1.training_model()
    training.compile(optimizer='adam', loss=vaem1.cost)
    training.fit(X_train, X_train,
                 batch_size=100,
                 nb_epoch=nb_epoch,
                 shuffle=True,
                 validation_data=(X_test, X_test)
                 )

    encoder = vaem1.encoder()
    encoder.save('./trained_model/encoder_m1.h5')
    decoder = vaem1.decoder()
    decoder.save('./trained_model/decoder_m1.h5')

CVAEとは

CVAEでは隠れ変数の1つにlabelを加えた確率モデルを考えます.
Semi-Supervised Learning with Deep Generative Models中でM2モデルと書かれている物です. 生成モデルとしては ${p(x|y, z)}$ を学習したいのですがcost関数が少し変化します.

${ \begin{align} log p(x) &\geq E_{q(z|x, y)} [logp(x|y,z)+logp(y)+logp(z)-logq(z|x, y)] \tag{1} \\ &= E_{q(z|x, y)} [logp(x|y,z)+logp(y)] - D_{KL}(\frac{q(z|x, y)}{q(z)}) \tag{2} \\ \end{align} }$

これがlabel付きデータのloss関数になります. 論文中で半教師あり学習を行う際にラベルなしデータに対するloss関数を導出していますが, 今回半教師あり学習は行わずにアナロジーだけ見るので解説はしません. 実装はしてあるので見てみてください.

論文中ではこのM2モデルにVAEで出てきた潜在変数 ${z}$ を入力変数として適用することでstacked VAEとしています.

VAEM2モデルのclass実装は下のようになります.

class VAEM2(object):
    def __init__(self, in_dim=50, cat_dim=10, hid_dim=300, z_dim=50, alpha=0):
        self.in_dim = in_dim
        self.cat_dim = cat_dim
        self.hid_dim = hid_dim
        self.z_dim = z_dim
        self.alpha = alpha
        self.x_l = Input((self.in_dim, ))
        self.x_u = Input((self.in_dim, ))
        self.y_l = Input((self.cat_dim, ))
        y_u0 = Input((self.cat_dim, ))
        y_u1 = Input((self.cat_dim, ))
        y_u2 = Input((self.cat_dim, ))
        y_u3 = Input((self.cat_dim, ))
        y_u4 = Input((self.cat_dim, ))
        y_u5 = Input((self.cat_dim, ))
        y_u6 = Input((self.cat_dim, ))
        y_u7 = Input((self.cat_dim, ))
        y_u8 = Input((self.cat_dim, ))
        y_u9 = Input((self.cat_dim, ))
        self.y_u = [y_u0, y_u1, y_u2, y_u3, y_u4, y_u5, y_u6, y_u7, y_u8, y_u9]
        self.z = Input((self.z_dim, ))

        ###############
        # q(z | x, y) #
        ###############
        x_branch = Sequential()
        x_branch.add(Dense(self.hid_dim, input_dim=self.in_dim))
        x_branch.add(CustomBatchNormalization())
        x_branch.add(Activation('softplus'))
        y_branch = Sequential()
        y_branch.add(Dense(self.hid_dim, input_dim=self.cat_dim))
        y_branch.add(CustomBatchNormalization())
        y_branch.add(Activation('softplus'))
        merged = Sequential([Merge([x_branch, y_branch], mode='concat')])
        merged.add(Dense(self.hid_dim))
        merged.add(CustomBatchNormalization())
        merged.add(Activation('softplus'))
        mean = Sequential([merged])
        mean.add(Dense(self.hid_dim))
        mean.add(CustomBatchNormalization())
        mean.add(Activation('softplus'))
        mean.add(Dense(self.z_dim))
        var = Sequential([merged])
        var.add(Dense(self.hid_dim))
        var.add(CustomBatchNormalization())
        var.add(Activation('softplus'))
        var.add(Dense(self.z_dim, activation='softplus'))
        self.q_z_xy = GaussianDistribution(self.z, givens=[self.x_l, self.y_l], mean_model=mean, var_model=var)

        ###############
        # p(x | y, z) #
        ###############
        y_branch = Sequential()
        y_branch.add(Dense(self.hid_dim, input_dim=self.cat_dim))
        y_branch.add(CustomBatchNormalization())
        y_branch.add(Activation('softplus'))
        z_branch = Sequential()
        z_branch.add(Dense(self.hid_dim, input_dim=self.z_dim))
        z_branch.add(CustomBatchNormalization())
        z_branch.add(Activation('softplus'))
        merged = Sequential([Merge([y_branch, z_branch], mode='concat')])
        merged.add(Dense(self.hid_dim))
        merged.add(CustomBatchNormalization())
        merged.add(Activation('softplus'))
        mean = Sequential([merged])
        mean.add(Dense(self.hid_dim))
        mean.add(CustomBatchNormalization())
        mean.add(Activation('softplus'))
        mean.add(Dense(self.in_dim))
        var = Sequential([merged])
        var.add(Dense(self.hid_dim))
        var.add(CustomBatchNormalization())
        var.add(Activation('softplus'))
        var.add(Dense(self.in_dim, activation='softplus'))
        self.p_x_yz = GaussianDistribution(self.x_l, givens=[self.y_l, self.z], mean_model=mean, var_model=var)

        ########
        # p(y) #
        ########
        self.p_y = CategoricalDistribution(self.y_l)

        ############
        # q(y | x) #
        ############
        inference = Sequential()
        inference.add(Dense(self.hid_dim, input_dim=self.in_dim))
        inference.add(CustomBatchNormalization())
        inference.add(Activation('softplus'))
        inference.add(Dense(self.hid_dim))
        inference.add(CustomBatchNormalization())
        inference.add(Activation('softplus'))
        inference.add(Dense(self.cat_dim, activation='softmax'))
        self.q_y_x = CategoricalDistribution(self.y_l, givens=[self.x_l], model=inference)

        ##########################
        # sample and reconstruct #
        ##########################
        self.sampling_z = self.q_z_xy.sampling(givens=[self.x_l, self.y_l])
        self.reconstruct_x_l = self.p_x_yz.sampling(givens=[self.y_l, self.sampling_z])

    def _KL(self, mean, var):
        return -1/2*K.mean(K.sum(1+K.log(K.clip(var, K._epsilon, 1/K._epsilon))-mean**2-var, axis=1))

    def label_cost(self, y_true, y_false):
        ###########
        # Labeled #
        ###########
        self.mean, self.var = self.q_z_xy.get_params(givens=[self.x_l, self.y_l])
        KL = self._KL(self.mean, self.var)
        logliklihood = -self.p_x_yz.logliklihood(self.x_l, givens=[self.y_l, self.sampling_z])-self.p_y.logliklihood(self.y_l)
        L = KL+logliklihood
        L = L+self.alpha*self.q_y_x.logliklihood(self.y_l, givens=[self.x_l])
        return L

    def cost(self, y_true, y_false):
        ###########
        # Labeled #
        ###########
        self.mean, self.var = self.q_z_xy.get_params(givens=[self.x_l, self.y_l])
        KL = self._KL(self.mean, self.var)
        logliklihood = -self.p_x_yz.logliklihood(self.x_l, givens=[self.y_l, self.sampling_z])-self.p_y.logliklihood(self.y_l)
        L = KL+logliklihood
        L = L+self.alpha*self.q_y_x.logliklihood(self.y_l, givens=[self.x_l])

        #############
        # UnLabeled #
        #############
        U = 0
        # marginalization
        for y in self.y_u:
            mean, var = self.q_z_xy.get_params(givens=[self.x_u, y])
            sampling_z = self.q_z_xy.sampling(givens=[self.x_u, y])
            U += self.q_y_x.prob(y, givens=[self.x_u])*(-self.p_x_yz.logliklihood(self.x_u, givens=[y, sampling_z])
                                                   -self.p_y.logliklihood(y)
                                                   +self._KL(mean, var)
                                                   +self.q_y_x.logliklihood(y, givens=[self.x_u])
                                                )
        return U+L

    def label_training_model(self):
        model = Model(input=[self.x_l, self.y_l], output=self.reconstruct_x_l)
        return model

    def training_model(self):
        model = Model(input=[self.x_l, self.y_l, self.x_u]+self.y_u, output=self.reconstruct_x_l)
        return model

    def encoder(self):
        model = Model(input=[self.x_l, self.y_l], output=self.mean)
        return model

    def decoder(self):
        decode = self.p_x_yz.sampling(givens=[self.y_l, self.z])
        model = Model(input=[self.y_l, self.z], output=decode)
        return model

    def classifier(self):
        inference = self.q_y_x.get_params(givens=[self.x_l])
        model = Model(input=self.x_l, output=inference)
        return model

実験

VAE

VAEモデルにmnistを入力して再構成を行いました.
実行コードは下のようになります.
kerasのdefaultのBatchNormalizationはtestの時もbatch単位計算してしまうmodeか, 層を再利用できないmodeしかなかったのでCustomBatchNormalizationという名前で再利用可能かつtest時に今までの平均と分散の指数移動平均を使用する層を作成しました.

from keras.models import load_model
from keras.datasets import mnist
import matplotlib.pyplot as plt
from custom_batchnormalization import CustomBatchNormalization

custom_objects={'CustomBatchNormalization': CustomBatchNormalization}

if __name__ == '__main__':
    (X_train, y_train), (X_test, y_test) = mnist.load_data()
    X_train = X_train.reshape(-1, 28*28)
    X_test = X_test.reshape(-1, 28*28)
    X_train = X_train/255.0
    X_test = X_test/255.0
    X_train[X_train > 0.5] = 1.0
    X_train[X_train <= 0.5] = 0.0
    X_test[X_test > 0.5] = 1.0
    X_test[X_test <= 0.5] = 0.0

    encoder = load_model('./trained_model/encoder_m1.h5', custom_objects=custom_objects)
    decoder = load_model('./trained_model/decoder_m1.h5', custom_objects=custom_objects)

    targets = X_train[0:5]

    latents = encoder.predict(targets, batch_size=5)
    reconstruct_images = decoder.predict(latents, batch_size=5)

    fig = plt.figure(figsize=(14, 14))
    for i, target in enumerate(targets):
        ax = fig.add_subplot(2, 5, i+1, xticks=[], yticks=[])
        ax.imshow(target.reshape(28, 28), 'gray')
    for i, reconstruct_image in enumerate(reconstruct_images):
        ax = fig.add_subplot(2, 5, 6+i, xticks=[], yticks=[])
        ax.imshow(reconstruct_image.reshape(28, 28), 'gray')
    plt.savefig('./images/reconstruct_m1.png')

上が元画像で下が再構成画像です. ある程度再構成できています.

f:id:ralo23:20160824180741p:plain

数字間アナロジー

${z}$ 上での多様体学習の様子を見てみます. target画像を2つ用意し, その2つを潜在変数空間上に落とし込み潜在空間上に直線を引いて直線上の ${z}$ を再構成します.

from keras.models import load_model
from keras.datasets import mnist
import numpy as np
import matplotlib.pyplot as plt
from custom_batchnormalization import CustomBatchNormalization

custom_objects = {'CustomBatchNormalization': CustomBatchNormalization}

if __name__ == '__main__':
    (X_train, y_train), (X_test, y_test) = mnist.load_data()
    X_train = X_train.reshape(-1, 28*28)
    X_test = X_test.reshape(-1, 28*28)
    X_train = X_train/255.0
    X_test = X_test/255.0
    X_train[X_train > 0.5] = 1.0
    X_train[X_train <= 0.5] = 0.0
    X_test[X_test > 0.5] = 1.0
    X_test[X_test <= 0.5] = 0.0

    encoder = load_model('./trained_model/encoder_m1.h5', custom_objects=custom_objects)
    decoder = load_model('./trained_model/decoder_m1.h5', custom_objects=custom_objects)

    target1 = X_train[0:1]
    target2 = X_train[8:9]

    latent1 = encoder.predict(target1, batch_size=1)
    latent2 = encoder.predict(target2, batch_size=1)

    fig = plt.figure(figsize=(14, 14))
    for i, d in enumerate(np.linspace(0, 1, 10)):
        latent = latent1+d*(latent2-latent1)
        reconstruct_image = decoder.predict(latent, batch_size=1)
        ax = fig.add_subplot(1, 10, i+1, xticks=[], yticks=[])
        ax.imshow(reconstruct_image.reshape(28, 28), 'gray')
    plt.savefig('./images/analogy_m1.png')

f:id:ralo23:20160824182031p:plain

５から１への変化が確認できます.

CVAE

論文中にあるM1モデル(VAE)との併用で実験を行います. VAEを使って全てのmnistトレーニングデータを ${z_1}$ の潜在空間に持って行きます. 次に潜在空間上のトレーニングデータを入力としてM2モデルをトレーニングします.

f:id:ralo23:20160826153356p:plain

VAEの時と同様に再構成してみます.

f:id:ralo23:20160826154721p:plain

再構成できています.

筆跡アナロジー

論文中では潜在変数に ${y}$ を追加したことによって ${z}$ が筆跡のようなものを捉えるようになったと書かれています.
実際に確認するために画像を ${z_2}$ の潜在変数空間に持って行き固定したまま, ラベル ${y}$ を0~9で変化させて再構成します.

コードは以下になります.

from keras.models import load_model
from keras.datasets import mnist
from keras.utils import np_utils
import numpy as np
import matplotlib.pyplot as plt
from custom_batchnormalization import CustomBatchNormalization

custom_objects = {'CustomBatchNormalization': CustomBatchNormalization}

if __name__ == '__main__':
    (X_train, y_train), (X_test, y_test) = mnist.load_data()
    X_train = X_train.reshape(-1, 28*28)
    X_test = X_test.reshape(-1, 28*28)
    X_train = X_train/255.0
    X_test = X_test/255.0
    X_train[X_train > 0.5] = 1.0
    X_train[X_train <= 0.5] = 0.0
    X_test[X_test > 0.5] = 1.0
    X_test[X_test <= 0.5] = 0.0
    y_train = np_utils.to_categorical(y_train, 10)
    y_test = np_utils.to_categorical(y_test, 10)

    encoder_m1 = load_model('./trained_model/encoder_m1.h5', custom_objects=custom_objects)
    decoder_m1 = load_model('./trained_model/decoder_m1.h5', custom_objects=custom_objects)
    encoder_m2 = load_model('./trained_model/encoder_m2.h5', custom_objects=custom_objects)
    decoder_m2 = load_model('./trained_model/decoder_m2.h5', custom_objects=custom_objects)

    X_targets = X_train[9:17]
    y_targets = y_train[9:17]
    z1 = encoder_m1.predict(X_targets, batch_size=8)
    z2 = encoder_m2.predict([z1, y_targets], batch_size=8)

    fig = plt.figure(figsize=(14, 14))
    for i, z in enumerate(z2):
        ax = fig.add_subplot(8, 11, 11*i+1, xticks=[], yticks=[])
        ax.imshow(X_targets[i].reshape(28, 28), 'gray')
        for j, y in enumerate(np.eye(10)):
            z1_reconstruct = decoder_m2.predict([y.reshape(1, -1), z2[i].reshape(1, -1)], batch_size=1)
            x_reconstruct = decoder_m1.predict(z1_reconstruct, batch_size=1)
            ax = fig.add_subplot(8, 11, 11*i+j+2, xticks=[], yticks=[])
            ax.imshow(x_reconstruct.reshape(28, 28), 'gray')
    plt.savefig('./images/analogy_m1_m2.png')

左１列が元の画像で右１０列が ${z_2}$ 固定の元ラベルを変えた画像です.

f:id:ralo23:20160826155817p:plain

元画像の筆跡を捉えているのが確認できます.

まとめ

深層学習をわりと自然に生成モデルの枠組みに適用したVAEの再現実験をしました.
最終的に深層学習で画像が生成できると言っても適当な画像が出てきたのでは意味がありません. 如何に狙った画像を従来の人間らしく, もしくは有用な形で出力できるかが大事になります. その点において生成モデルは人間の狙いを組込みやすいモデルなのではないかと思っています.

最後に今回の実装に使ったコードはhttps://github.com/rarilurelo/keras-VAEに置いてあります.
間違っている部分わかりづらい部分ありましたら教えて下さい.

rarilureloの日記

筋肉が学んだことを書きます. 機械学習とか.